One to One Functions - Graph, Examples | Horizontal Line Test
What is a One to One Function?
A one-to-one function is a mathematical function in which each input corresponds to a single output. So, for each x, there is only one y and vice versa. This signifies that the graph of a one-to-one function will never intersect.
The input value in a one-to-one function is the domain of the function, and the output value is known as the range of the function.
Let's examine the examples below:
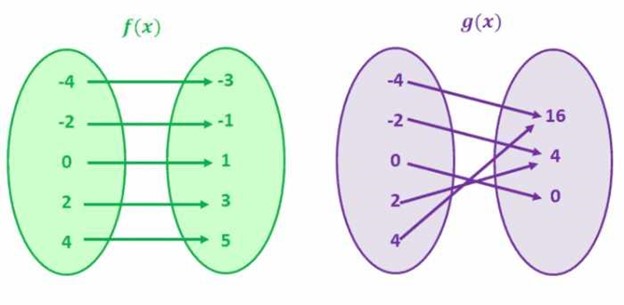
For f(x), every value in the left circle corresponds to a unique value in the right circle. In conjunction, any value in the right circle corresponds to a unique value on the left side. In mathematical terms, this implies every domain holds a unique range, and every range has a unique domain. Therefore, this is a representation of a one-to-one function.
Here are some more representations of one-to-one functions:
-
f(x) = x + 1
-
f(x) = 2x
Now let's examine the second image, which displays the values for g(x).
Pay attention to the fact that the inputs in the left circle (domain) do not own unique outputs in the right circle (range). For example, the inputs -2 and 2 have equal output, that is, 4. Similarly, the inputs -4 and 4 have the same output, i.e., 16. We can comprehend that there are equivalent Y values for numerous X values. Hence, this is not a one-to-one function.
Here are additional representations of non one-to-one functions:
-
f(x) = x^2
-
f(x)=(x+2)^2
What are the properties of One to One Functions?
One-to-one functions have the following qualities:
-
The function owns an inverse.
-
The graph of the function is a line that does not intersect itself.
-
The function passes the horizontal line test.
-
The graph of a function and its inverse are equivalent concerning the line y = x.
How to Graph a One to One Function
To graph a one-to-one function, you will need to determine the domain and range for the function. Let's look at a straight-forward example of a function f(x) = x + 1.
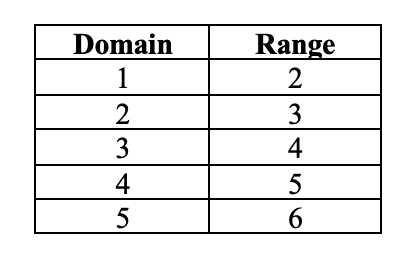
Immediately after you have the domain and the range for the function, you need to graph the domain values on the X-axis and range values on the Y-axis.
How can you evaluate whether a Function is One to One?
To indicate if a function is one-to-one, we can apply the horizontal line test. Once you chart the graph of a function, draw horizontal lines over the graph. If a horizontal line intersects the graph of the function at more than one place, then the function is not one-to-one.
Because the graph of every linear function is a straight line, and a horizontal line doesn’t intersect the graph at more than one spot, we can also conclude all linear functions are one-to-one functions. Remember that we do not apply the vertical line test for one-to-one functions.
Let's study the graph for f(x) = x + 1. Once you chart the values of x-coordinates and y-coordinates, you ought to review if a horizontal line intersects the graph at more than one point. In this instance, the graph does not intersect any horizontal line more than once. This signifies that the function is a one-to-one function.
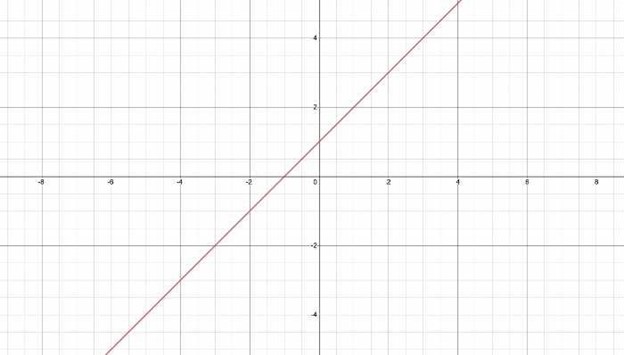
Subsequently, if the function is not a one-to-one function, it will intersect the same horizontal line multiple times. Let's examine the graph for the f(y) = y^2. Here are the domain and the range values for the function:
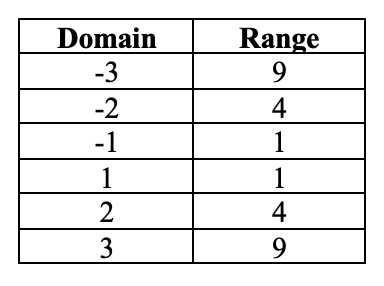
Here is the graph for the function:
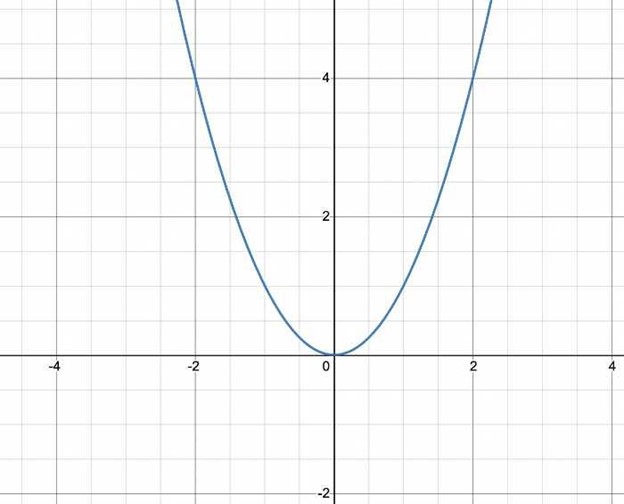
In this case, the graph intersects numerous horizontal lines. For instance, for either domains -1 and 1, the range is 1. Additionally, for either -2 and 2, the range is 4. This implies that f(x) = x^2 is not a one-to-one function.
What is the opposite of a One-to-One Function?
Considering the fact that a one-to-one function has only one input value for each output value, the inverse of a one-to-one function also happens to be a one-to-one function. The inverse of the function essentially reverses the function.
For example, in the event of f(x) = x + 1, we add 1 to each value of x as a means of getting the output, in other words, y. The opposite of this function will remove 1 from each value of y.
The inverse of the function is f−1.
What are the characteristics of the inverse of a One to One Function?
The properties of an inverse one-to-one function are no different than all other one-to-one functions. This implies that the opposite of a one-to-one function will have one domain for every range and pass the horizontal line test.
How do you determine the inverse of a One-to-One Function?
Finding the inverse of a function is very easy. You simply need to change the x and y values. Case in point, the inverse of the function f(x) = x + 5 is f-1(x) = x - 5.
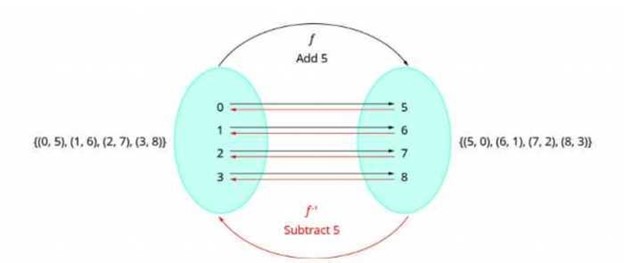
Just like we discussed previously, the inverse of a one-to-one function reverses the function. Considering the original output value required adding 5 to each input value, the new output value will require us to subtract 5 from each input value.
One to One Function Practice Examples
Consider these functions:
-
f(x) = x + 1
-
f(x) = 2x
-
f(x) = x2
-
f(x) = 3x - 2
-
f(x) = |x|
-
g(x) = 2x + 1
-
h(x) = x/2 - 1
-
j(x) = √x
-
k(x) = (x + 2)/(x - 2)
-
l(x) = 3√x
-
m(x) = 5 - x
For any of these functions:
1. Determine whether the function is one-to-one.
2. Draw the function and its inverse.
3. Figure out the inverse of the function algebraically.
4. Indicate the domain and range of every function and its inverse.
5. Apply the inverse to find the solution for x in each formula.
Grade Potential Can Help You Learn You Functions
If you are facing difficulties trying to understand one-to-one functions or similar concepts, Grade Potential can connect you with a one on one tutor who can assist you. Our Seattle math tutors are skilled professionals who help students just like you improve their understanding of these types of functions.
With Grade Potential, you can study at your individual pace from the convenience of your own home. Schedule a call with Grade Potential today by calling (206) 339-6328 to get informed about our educational services. One of our consultants will contact you to better determine your requirements to find the best tutor for you!




